Identités Remarquables - Factorisation

Comment factoriser une expression avec les identités remarquables?

1. Qu'est-ce que factoriser (Rappel)?

Factoriser, c’est transformer une somme ou une différence en un produit. Cela permet de simplifier des calculs ou de résoudre des équations.

Exemple : $x^2 - 4 = (x-2)(x+2)$

2. Les Identités Remarquables

Les identités remarquables sont des outils clés pour factoriser des expressions algébriques. Il y en a trois principales :

1. Carré d’une somme :

   $$(a+b)^2 = a^2 + 2ab + b^2$$
   

   Lors de la factorisation : $a^2+2ab+b^2=(a+b{)}^2$

2. Carré d’une différence :

   $$(a-b)^2 = a^2 - 2ab + b^2$$
   

   Lors de la factorisation : $a^2 - 2ab + b^2 = (a-b)^2$
   

3. Différence de deux carrés :

   $$(a-b)(a+b) = a^2 - b^2$$
   

   Lors de la factorisation : $a^2-b^2=(a-b)(a+b)$

---

3. Comment identifier l'identité remarquable à utiliser ?

Étape 1 : Identifier la forme de l’expression

• Si l’expression comporte trois termes, il s’agit probablement d’un carré d’une somme ou d’un carré d’une différence.

  • Vérifiez si le premier et le dernier termes sont des carrés parfaits ($a^2, b^2$).
  • Vérifiez si le terme du milieu correspond à $2ab$ ou $-2ab$.

• Si l’expression comporte deux termes, il s’agit probablement d’une différence de deux carrés.

  • Vérifiez si les deux termes sont des carrés parfaits séparés par un signe $-$.

Étape 2 : Factoriser

Utilisez la formule appropriée pour écrire l'expression sous forme factorisée.

---

4. Exemples

Exemple 1 : Carré d’une somme

Factoriser $x^2 + 6x + 9$.

1. Identifier : Le premier terme $x^2$  et le dernier terme $9$ sont des carrés parfaits : $x^2 = x^2$ donc a² = x² , $9 = 3^2$ , donc b² = 3²
2. Vérifier le terme du milieu : $6x = 2 \times x \times 3$. donc 2ab = 6x
3. Conclusion : l'expression à factoriser correspond à la formule a² + 2ab + b² = (a = b)² donc,  ${\mathrm{<b>x</b>}}^{\mathrm{<b>2</b>}}<b>+</b>\mathrm{<b>6</b>}\mathrm{<b>x</b>}<b>+</b>\mathrm{<b>9</b>}<b>=</b><b>(</b>\mathrm{<b>x</b>}<b>+</b>\mathrm{<b>3</b>}{<b>)</b>}^{\mathrm{<b>2</b>}}$

---

Exemple 2 : Carré d’une différence

Factoriser $y^2 - 10y + 25$

1. $\mathrm{<span\; class="katex"\; style="font-family:\; courier;\; font-size:\; large;"><span\; aria-hidden="true"\; class="katex-html"><span\; class="base"><span\; class="mord"><span\; class="msupsub"><span\; class="vlist-t"><span\; class="vlist-r"><span\; class="vlist"><span\; class="sizing\; reset-size6\; size3\; mtight"><span\; class="mord\; mtight">y\; ²et\; 25\; =\; 5² </span></span></span></span></span></span></span></span></span>sont\; des\; carrés\; parfaits.</span>}$
2. Vérifier le terme du milieu : $-10y=2\times y\times (-5)$.
3. Conclusion : ${\mathrm{<b>y</b>}}^{\mathrm{<b>2</b>}}<b>-</b>\mathrm{<b>10</b>}\mathrm{<b>y</b>}<b>+</b>\mathrm{<b>25</b>}$
   

---

Exemple 3 : Différence de deux carrés

Factoriser $16x^2 - 9$

1. Identifier : $16x^2 = (4x)^2$ et 9 = 3²
2. Reconnaître une différence de carrés (a² - b²): $16x^2 - 9 = (4x-3)(4x+3)$
   

---

5. Cas particuliers

Si l’expression ne correspond pas directement à une identité remarquable, essayez de regrouper les termes ou de mettre un facteur commun en évidence.

Exemple : $2x^2 + 8x + 8$

1. Factorisez par $2$ : $2(x^2 + 4x + 4)$
   
2. Puis factorisez l’intérieur : $2(x+2)^2$
   

---

6. Entraînez-vous

Essayez de factoriser les expressions suivantes :

1. $x^2 - 25$
   
2. $9y^2 + 12y + 4$
3. $4a^2 - 16$
   

---

Correction :

1. $x^2 - 25 = (x-5)(x+5)$
   
2. $9y^2 + 12y + 4 = (3y+2)^2$
   
3. $$4a2−16=4(a2−4)=4(a−2)(a+2)4a^2 - 16 = 4(a^2 - 4) = 4(a-2)(a+2)
   

Inéquations

Définition

Une inéquation est une équation avec un symbole <, ≤, > 

ou ≥ à la place du signe =

 Vocabulaire des symboles  <, ≤, >, ≥

• < : Strictement inférieur à
• ≤ : Inférieur ou égal
• > : Strictement supérieur à
• ≥ : Supérieur ou égal

Résoudre une inéquation

Pour résoudre une inéquation, il faut trouver toutes 

les valeurs de l’inconnue qui rendent l’inégalité vraie. 

• Une inéquation se résout comme une équation, sauf qu'au lieu d'avoir une égalité, nous aurons une inégalité avec les symboles > ou < 

Exemple:

Résoudre l'inéquation suivante

x + 3 > 5 : pour résoudre cette inéquation, il faut trouver  le nombre qu'on doit ajouter à 3 pour que le résultat soit supérieur à 5

x + 3 - 3 > 5 - 3

x > 2

Vérification: On remplace x par un nombre strictement supérieur à 2 , par exemple 3

On remplace x par 3

3 + 3 = 6

6 est bien supérieur à 5

Propriétés

 Addition et soustraction 

 On ne change pas le sens d’une inégalité quand on ajoute (ou on soustrait) un même nombre aux deux membres. 

exemple si x > 7, alors

 x + 2 > 7 + 2

 x + 2 > 9

Multiplication et division : 

1er cas

• On ne change pas le sens d’une inégalité quand on multiplie (ou on divise) les deux membres par un même nombre POSITIF. Exemple : 

Si X > 7                         Si X < 7 

Alors  X x 2 > 7 x 2             Alors: X x 2 < 7 x 2  

          2X > 14                       2X  < 14 

Si x > 7  alors:                  Si x < 7 alors:                         

                                                                      

2ème cas

• On change le sens d’une inégalité quand on multiplie ou on divise les deux membres par un même nombre NÉGATIF. 

Exemple

Si X > 7  , alors                          

  X x(-2) > 7 x (-2)          

          - 2X < - 14                      

            

Si X  > 7  alors:                      

      

Exercice corrigé

2x < -4

  2x/2 < -4/2

   x < - 2 

Plus d'exercices Corrigés

  

PGCD de deux nombres

• Division Euclidienne

Effectuer une division euclidienne de a par b c'est trouver deux entiers q et r tel que:

a ÷  b = q + r où r < b  où q est le quotient et r est le reste

a est appelé le dividende et b est le diviseur

• Calcul du PGCD

Définition:

Le PGCD de deux nombres est le plus grand diviseur commun à ces 2 nombres. On le note PGCD de (a ; b)

a) Trouver le PGCD grâce à l'algorithme d'Euclide

Cette méthode consiste à diviser le plus grand nombre par le plus petit, ensuite on divise  le quotient et le reste de la division précédente  et on recommence . on ne s'arrête que lorsque le reste est nul. Le PGCD est le dernier reste non nul

Exemple: trouver le PGCD de (621 ; 405)

Le dernier reste non nul est 27, par conséquent le PGCD de 621 et 405 est 27

Pour vous entrainer, faites ce QUIZ

Notions de fonctions

 Définition

Une fonction est un processus mathématique qui à tout nombre x fait correspondre un nombre qu'on note f(x).

On note : f : x ⟼ f(x)

Exemple:

l'aire du rectangle ci-dessous dépend de la valeur de x(sa largeur

A : x ⟼ A(x)=5x   

           

• Images et antécedents

​Définition:

f(x) est l’image de x par la fonction f. x est l’antécédent de f(x) par la fonction f. 

 - x s'appelle l'antécédent de f(x)

 - f(x) s'appelle l'image de x

Exemple : f : x ⟼ f(x) = 4x f(2) = 8 , l'image de 2 par f est  8 et  l'antécédent de 8 par  f est 2

Représentation graphique d'une fonction

Définition: 

 La représentation graphique d’une fonction est l’ensemble des points de coordonnées (x ; y) telles que y = f(x). C’est donc l’ensemble des points de coordonnées (x ; f(x)) ou (x,y)

Pour tracer la représentation

1. Etablir un tableau de valeurs 
2. Tracer un repère 
3. Placer les points de coordonnées (x ;f(x)) 
obtenus dans le tableau 
4. Relier les points 

Exemple: soit f : x ⟼ f(x) = x -1

1. On établit un tableau des valeurs

x	-2	-1	0	1	2
f(x)	-3	-2	-1	0	1

  2. On trace  un repère

Cosinus D'un Angle

Définition 

Dans un triangle rectangle, le cosinus d'un angle aigu est égal au quotient du côté adjacent à cet angle (l'angle aigu) sur l'hypoténuse.

 

Le triangle ABC rectangle en B, écrire la formule donnant le cosinus de l'angle  :

- AB  est le côté adjacent à l'angle aigu Â

- AC est l'hypoténuse( le côté le plus grand du triangle)

Donc :

 

Pourquoi utiliser la formule du cosinus?

1. Pour calculer la mesure d'une longueur( côté adjacent d'un angle ou l'hypoténuse).

​Exemple: soit le triangle MNP rectangle en M, l'angle N = 30°,

NP = 6 cm. Calculer la longueur de MN arrondie au dixième près?

Réponse: 

   

 

  

 

2. Pour Calculer la mesure d'un angle

Exemple: Soit un triangle RST rectangle en R, RS = 4 cm, ST = 6 cm

Calculer la mesure de L'angle S au degré?

 

Réponse:

  

 

Pour trouver la mesure de l'angle  il faut utiliser la fonction cos^-1 de la calculatrice. 

Elle s’obtient souvent en tapant sur les touches

 

Dans l'exemple que nous venons de voir pour trouver la mesure de l'angle S, nous avons taper cos^-1(4/6)

 

Remarque: 

La formule du cosinus d’un angle dans un triangle rectangle nous permet de calculer soit la longueur d’un côté(Exemple1), soit un des angles de ce triangle(Exemple2).

 

Bientôt La suite de la leçon, en attendant  entraînez-vous à répondre au Quiz ici

 

 

                            

Les Fonctions affines

 

La fonction affine de coefficients a et b et noté x → ax + b, on la désigne souvent par une lettre par exemple f et on peut la noter aussi sous cette forme: f(x) = ax + b

Exemple: la fonction affine g, de coefficients 3 et -2 s'écrit : g(x) = 3x - 2

Remarque:

• Si b = o, On obtiens une fonction sous la forme de f(x)= ax ce qui correspond à une fonction linéaire. D'où une fonction linéaire est aussi une fonction linéaire avec b = 0

 

• Si a = 0  on obtiens une fonction constante f(x) = b

 

• Si a = b = 0 on obtiens une fonction nulle f(x) = 0

Représentation graphique

Dans un repère, la représentation graphique d'une fonction affine est une droite. l'équation de cette de droite s'écrit sous la forme: y = ax + b.

• x est l'abscisse et y et l'ordonnée
• a s'appelle le coefficient directeur et b s'appelle l'ordonnée à l'origine

 

Exercice d'application: dans un repère, trace la représentation graphique de la fonction affine f x → -x +2

Méthode

• On donne 2 ou 3 valeurs à x supposons 0, 1 et 2
• On calcule leurs images par la fonction f: f(o) = -0 + 2 = 2, f(1) = -1 + 2 = +1, f(2) = - 2 + 2 = 0
• Donc l'image de 0 est 2, l'mage de 1 est - 3 et l'image 2 est -8 

x	0	1	2
f(x)	2	+1	0

 

 

 

Maths Collège - Les Puissances

1.  Puissance d'un nombre 

la puissance $\text{n-ième}$start text, n, negative, i, e, with, \`, on top, m, e, end text d'un nombre est le produit de $n$n facteurs égaux à ce nombre.
 On appelle " a puissance n" an  tel que :

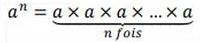(n est appelé aussi exposant)

Exemple: 
 5² = 5x5, ça se lit 5 au carré , ici on a multiplié 5 par lui même , n = 2

5⁴ = 5 x 5x 5 x 5, ici  n = 5

 
Remarque:
Attention -3² n'est pas égale à (-3)² 
-3² = - 9  le résultat est négatif
(- 3)²= 9  le résultat est positif

2.  Puissance de 10
Soit n un entier supérieur à 1, Le produit 10 x 10 x 10 x 10…..x 10 s note 10ⁿ  et se lit  " 10 puissance n ".
A retenir : 10° = 1 

Propriétés : Soit n un entier positif.

Propriété 1: pour multiplier un nombre décimal par 10ⁿ, on déplace la virgule de n rangs vers la droite.

Propriété 2 : pour multiplier un nombre décimal par 10⁻ⁿ, on déplace la virgule de n rangs vers la gauche

Exemples:

application de la propriété 1 

Donne l'écriture décimal de A = 65,23 x 10⁶

- 65,23 x 10⁶ = 65230000,  n = 6, on décale donc la virgule de 6 rangs vers la droite .

application de la propriété 2

 Donne l'écriture décimal de A = 65,23 x 10⁻⁶

- 65,23 x 10⁻⁶ = 0,00006523,  on déplace la virgule de 6 rangs vers la gauche si l'exposant négatif

A = 0,00006523

 1. Règle Puissance de 10 - Produit

Soit 2 nombres entiers relatifs  m et p

Exemple:

10²x 10⁴ = 10²⁺⁴ =10⁶

2. Règle Puissance de 10 - Quotient

Exemple: 

3. Règle Puissance de 10 - Puissance d'une puissance

Exemple: 
(10³)² = 10³ˣ² = 10⁶

Ecriture Scientifique
Définition : L’écriture scientifique d’un nombre est l’écriture de ce nombre sous la forme a × 10ⁿ  où a est un nombre décimal ayant un seul chiffre non nul avant la virgule  et n un nombre entier relatif
Exemple : donne la notation scientifique de A = 8562
L'écriture scientifique de A = 8562 est:
A = 8,562 x 10³