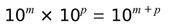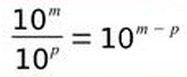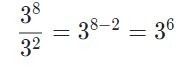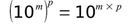la puissance start text, n, negative, i, e, with, \`, on top, m, e, end text d'un nombre est le produit de n facteurs égaux à ce nombre.
On appelle " a puissance n" an tel que :
Exemple:
5² = 5x5, ça se lit 5 au carré , ici on a multiplié 5 par lui même , n = 2
5⁴ = 5 x 5x 5 x 5, ici n = 5
On appelle " a puissance n" an tel que :
5² = 5x5, ça se lit 5 au carré , ici on a multiplié 5 par lui même , n = 2
5⁴ = 5 x 5x 5 x 5, ici n = 5
Remarque:
Attention -3² n'est pas égale à (-3)²
-3² = - 9 le résultat est négatif
(- 3)²= 9 le résultat est positif
2. Puissance de 10
Soit n un entier supérieur à 1, Le produit 10 x 10 x 10 x 10…..x 10 s note 10ⁿ et se lit " 10 puissance n ".
A retenir : 10° = 1
Propriétés : Soit n un entier positif.
Propriété 1: pour multiplier un nombre décimal par 10ⁿ, on déplace la virgule de n rangs vers la droite.
Propriété 2 : pour multiplier un nombre décimal par 10⁻ⁿ, on déplace la virgule de n rangs vers la gauche
Exemples:
application de la propriété 1
Donne l'écriture décimal de A = 65,23 x 10⁶
- 65,23 x 10⁶ = 65230000, n = 6, on décale donc la virgule de 6 rangs vers la droite .
application de la propriété 2
Donne l'écriture décimal de A = 65,23 x 10⁻⁶
- 65,23 x 10⁻⁶ = 0,00006523, on déplace la virgule de 6 rangs vers la gauche si l'exposant négatif
A = 0,00006523
1. Règle Puissance de 10 - Produit
Soit 2 nombres entiers relatifs m et p
Exemple:
10²x 10⁴ = 10²⁺⁴ =10⁶
2. Règle Puissance de 10 - Quotient
Exemple:
3. Règle Puissance de 10 - Puissance d'une puissance
Exemple:
(10³)² = 10³ˣ² = 10⁶
Ecriture Scientifique
Définition : L’écriture scientifique d’un nombre est l’écriture de ce nombre sous la forme a × 10ⁿ où a est un nombre décimal ayant un seul chiffre non nul avant la virgule et n un nombre entier relatif
Exemple : donne la notation scientifique de A = 8562
L'écriture scientifique de A = 8562 est:
A = 8,562 x 10³


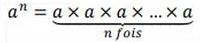 (n est appelé aussi exposant)
(n est appelé aussi exposant)