Cours Vitesse Moyenne, Distance, Temps

Vitesse moyenne

Définition:

La vitesse moyenne V d'un mobile qui a parcouru la distance d pendant la durée t est égale au quotient dt .

 

v=dt

Distance

  La distance d parcourue par un mobile à la vitesse moyenne v pendant la durée t est égale au produit v×t

 

d=v×t

Durée:

Définition: 

La durée t du parcours d'un mobile à la vitesse moyenne v sur une distance d est égale au quotient dv 

 

t=dv

Exercice 1:

Une voiture parcourt 385km en 3h et 30mn. Quelle est sa vitesse moyenne ?

Corrigé

Il faut d'abord convertir 30mn en heure = 0,5h , t =3,5h

 V= d/t 

 V= 385÷ 3,5 

 V = 110 

La vitesse moyenne est de 110.km/h

Exercice 2 :

 Une motard roule à 90km/h pendant 2h . Quelle  distance a-t-il parcourue ? 

Corrigé

d = V ×  t = 90 × 2 

d  = 180km 

La distance parcourue est de 180km. 

Exercice 3 : 

Un camion a parcouru 210 km  à une vitesse moyenne de 70 km/h. Combien de temps a-t-il mis pour parcourir cette distance ?

Corrigé

t = d/V 

t = 210 ÷ 70 = 3

Le temps mis pour parcourir cette distance est de

Triangles - Milieux et Parallèles

 Milieux et parallèles

Propriété 1: 

Dans un triangle, si une droite passe par les milieux de deux côtés alors elle est parallèle au troisième côté.

Remarque: cette propriété permet de démontrer que deux droites sont parallèles

Exemple: soit le triangle ABC, M est le milieu de AB et N est le milieu de AC. Démontrer que (MN) et (BC) sont parallèles

                              

Rédaction:

Dans le triangle ABC M est le milieu du côté AB et N est le milieu du côté AC

or on sait que si une droite passe par les milieux de deux côtés alors elle est parallèle au troisième côté.

On en déduit que (MN) // (AC)

Propriété 2

Si dans un triangle , une droite passe par le milieu d'un côté et est parallèle au deuxième alors elle passe le milieu du troisième côté.

La droite (d) est parallèle à AC

Rédaction:

Dans le triangle ABC, M est le milieu de [AB], la droite (d) est parallèle à [BC], or on sait que si une droite passe par le milieu d'un côté d'un triangle et est parallèle au deuxième côté alors elle coupe le troisième en son milieu, on en déduit que  (d) coupe [AC] en son milieu.

Propriété 3

Si dans un triangle, un segment coupe les milieux des deux côtés alors sa longueur est égale à la moitié de celle du troisième côté.

Rédaction:

Dans le triangle ABC, [MN] coupe [AB] et [AC] en leur milieu, or on sait que si un segment coupe deux côtés d'un triangle en leur milieu alors sa longueur est égale à la moitié de celle du troisième côté,

on en déduit que [MN] est égal à la moitié de [BC]

AM = AC  ÷ 2

Entraine- toi en faisant ces EXERCICES

Les angles - Maths 5ème

 Angles adjacents

Deux angles sont adjacents sont deux angles qui ont :

• ont le même sommet
• ont un côté en commun
• sont situés de part et d’autre du côté en commun.

Les angles Complémentaires

Deux angles sont complémentaires lorsque la somme de leurs mesures est égale à 90°

Les Angles opposés par le sommet

Deux angles sont opposés par le sommet sont deux angles :

• qui ont le même sommet
• Dont Les côtés de l’un sont le prolongement des côtés de l’autre.
• qui ont la même mesure

Les angles supplémentaires

Deux angles sont supplémentaires lorsque la somme de leurs mesures est égale à 180°

Médiatrice d'un Segment

 

Médiatrice d'un Segment

Définition

La médiatrice d'un segment est la droite qui coupe ce segment en son milieu et perpendiculairement

Puisque la médiatrice (d) coupe le segment [AB] en son milieu alors AM = MB

NB:  la médiatrice d'un segment est aussi l'axe de symétrie de ce segment

Propriété : Tous les points de la médiatrice d'un segment [AB] sont à égale distance des points A et B.

Exemple: le point C appartient à la droite

Puisque le point C est à égale distance de A et de B alors AC = BC

Méthodes de construction de la médiatrices:

Il existe deux méthodes pour construire la médiatrice d'un segment: au compas ou l'aide d'une équerre:

1 Au compas

•  Prendre un écartement de compas plus grand que la moitié du segment
•  Placer la pointe sèche du compas en A et tracer un arc de cercle de part et d'autre du segment
•  Faire de même, pointe sèche en B
• A l'aide d'une règle, tracer une droite reliant M et N, les points d'intersections des arcs de cercle,. cette droite est  la médiatrice de ce segment

2 A l'équerre

• placer le milieu du segment avec la règle graduée 
• tracer avec l'équerre la perpendiculaire au segment passant par le milieu.

Pour savoir comment construire une médiatrice, je vous invite à regarder cette vidéo↓

Comment Construire Une bissectrice?

 Définition:

Une bissectrice est la demi droite qui partage un angle en 2 angles adjacents de même mesure.

Etapes pour Construire une bissectrice à l'aide du compas:

• Ouvrir le compas et conserver cette ouverture pour toutes les étapes de construction.
• Placer la pointe du compas sur le sommet de l'angle et tracer un arc qui coupe les deux côtés de l'angle.
• Placer la pointe du compas sur une intersection de l'arc de cercle et d'un côté de l'angle.
• Tracer un nouvel arc dans l'ouverture de l'angle.
• Placer la pointe du compas sur une intersection de l'arc de cercle et l'autre côté de l'angle.
• Tracer un 2ème arc dans l'ouverture de l'angle formant une intersection avec le 1er arc
• À l'aide d'une règle, tracer la droite qui relie le sommet de l'angle au point d'intersection des deux derniers arcs tracés

La  demie droit AD est la bissectrice de l'angle AÔB

Etape pour tracer une bissectrice à l'aide du rapporteur

1. Avec un rapporteur d'angle, mesurer l'angle 
2. Diviser la valeur de l'angle en deux.
3. A l'aide du rapporteur , reporter la valeur de l'angle trouvé dans l'étape 2 et le repérer avec un point
4. A l'aide de la règle, tracer la demie droite passant par ce point et le sommet de l'angle, cette demie droite est la bissectrice de cette angle

Dans la vidéo ci-dessous, vous allez apprendre à construire une bissectrice à l'aide du compas

Les Identités Remarquables

Les identités remarquables servent en général à simplifier

certaines écritures, à factoriser ou à développer des expressions.

Elles sont au nombre de 3:

• Le carré de la somme de 2 nombres

Propriété: le carré de la somme de deux nombres égale la somme de leurs carrés augmentée du double produit de ces deux nombres.

(a + b)² = a² + 2ab + b²

Démonstration:

(a + b)² = (a + b)(a + b) = a² + a b + b a + b² = a² + 2 a b + b²

• Le carré de la différence de 2 nombres

Le carré de la différence de deux nombres égale la somme de leurs carrés diminuée du double du produit de ces deux nombres. 

(a - b)² = a²- 2ab + b²

Démonstration:

(a - b)² = (a - b)(a - b) = a² - a b - b a + b² = a² + 2 a b + b²

• Produit de la somme et de la différence de 2 nombres

( a + b ) ( a – b ) = a² – b² 

Démonstration:

(a + b)(a - b)  = a² - a b + b a - b² = a²- b²

Identités Remarquables en vidéo - 1ère Partie

(a + b)² = a² + 2ab + b²

Identités Remarquables - 2ème Partie

Dans cette vidéo nous allons aborder les 2 autres identités remarquables:

(a - b)² = a²- 2ab + b²

(a + b)(a - b) = a² - b²

La première identité remarquable est dans cette vidéo

 

Entiers et Rationnels

1/ Les nombres entiers

• Les nombres entiers naturels

​Définition

les nombres entiers naturels sont des nombres qui s'écrivent sans virgule, ni barre de fraction ou radical

Exemple: 24;346, 200.....

• Les nombres entiers relatifs

​Définition

Les nombres entiers relatifs sont les nombres positifs et négatifs qui peuvent s'écrire sans virgule , ni  barre de fraction, ni radical...).

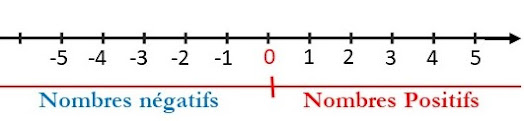
les signes positif (+) et négatif(-) indique la position du nombre sur un axe par rapport à 0

• Les nombres positifs sont situés à droite de 0
• Les nombres négatif sont situés 0 gauche de 0
• Le nombre 0 est le seul nombre qui est à la fois positif et négatif

 

2/Les nombres décimaux

Définition

Un nombre décimal est un nombre composé d'une partie entière comprenant des chiffres situés avant la virgule ; et d'une partie décimale composée de chiffres situés après la virgule.

 Exemple 3,5 ; 56,2 0,507 ....etc

3/ Les nombres Rationnels

Définition

Un nombre « rationnel » est un nombre qui peut s'écrire sous la forme d'un quotient de deux nombres entiers relatifs a/b.

• Multiples Diviseurs :

Définition :

a et b sont deux entiers naturels (non nuls). SI a=b × c avec c un entier ALORS  b est un diviseur de a et a est un multiple de b. Exemple : 15 = 5 × 3 donc 15 est un multiple de 5 ; 15 est divisible par 5 et par 5 et 3 sont appelés diviseurs

• PGCD de deux nombres

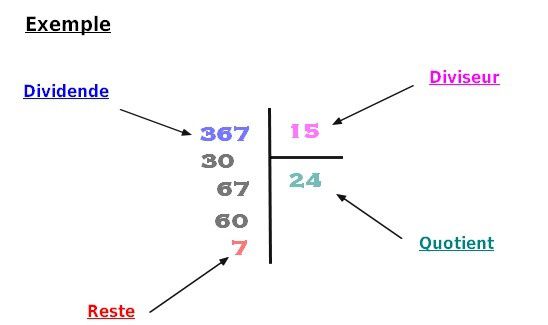
Division Euclidienne

Effectuer une division euclidienne de a par b c'est trouver deux entiers q et r tel que a : b = q + r où r < b  où q est le quotient et r est le reste

a est appelé le dividende et b est le diviseur

 

• Calcul du PGCD 

   Définition

Le PGCD de deux nombres est le plus grand diviseurs commun à ces 2 nombres. On le note PGCD (a ; b)

Pour la méthode de calcul du PGCD, je vous invite à aller voir la ici: PGCD de deux nombres