Triangles - Propriétés

 Les triangles  - Propriétés à retenir

Inéquations

Définition

Une inéquation est une équation avec un symbole <, ≤, > 

ou ≥ à la place du signe =

 Vocabulaire des symboles  <, ≤, >, ≥

• < : Strictement inférieur à
• ≤ : Inférieur ou égal
• > : Strictement supérieur à
• ≥ : Supérieur ou égal

Résoudre une inéquation

Pour résoudre une inéquation, il faut trouver toutes 

les valeurs de l’inconnue qui rendent l’inégalité vraie. 

• Une inéquation se résout comme une équation, sauf qu'au lieu d'avoir une égalité, nous aurons une inégalité avec les symboles > ou < 

Exemple:

Résoudre l'inéquation suivante

x + 3 > 5 : pour résoudre cette inéquation, il faut trouver  le nombre qu'on doit ajouter à 3 pour que le résultat soit supérieur à 5

x + 3 - 3 > 5 - 3

x > 2

Vérification: On remplace x par un nombre strictement supérieur à 2 , par exemple 3

On remplace x par 3

3 + 3 = 6

6 est bien supérieur à 5

Propriétés

 Addition et soustraction 

 On ne change pas le sens d’une inégalité quand on ajoute (ou on soustrait) un même nombre aux deux membres. 

exemple si x > 7, alors

 x + 2 > 7 + 2

 x + 2 > 9

Multiplication et division : 

1er cas

• On ne change pas le sens d’une inégalité quand on multiplie (ou on divise) les deux membres par un même nombre POSITIF. Exemple : 

Si X > 7                         Si X < 7 

Alors  X x 2 > 7 x 2             Alors: X x 2 < 7 x 2  

          2X > 14                       2X  < 14 

Si x > 7  alors:                  Si x < 7 alors:                         

                                                                      

2ème cas

• On change le sens d’une inégalité quand on multiplie ou on divise les deux membres par un même nombre NÉGATIF. 

Exemple

Si X > 7  , alors                          

  X x(-2) > 7 x (-2)          

          - 2X < - 14                      

            

Si X  > 7  alors:                      

      

Exercice corrigé

2x < -4

  2x/2 < -4/2

   x < - 2 

Plus d'exercices Corrigés

  

Médiatrice d'un Segment

 

Médiatrice d'un Segment

Définition

La médiatrice d'un segment est la droite qui coupe ce segment en son milieu et perpendiculairement

Puisque la médiatrice (d) coupe le segment [AB] en son milieu alors AM = MB

NB:  la médiatrice d'un segment est aussi l'axe de symétrie de ce segment

Propriété : Tous les points de la médiatrice d'un segment [AB] sont à égale distance des points A et B.

Exemple: le point C appartient à la droite

Puisque le point C est à égale distance de A et de B alors AC = BC

Méthodes de construction de la médiatrices:

Il existe deux méthodes pour construire la médiatrice d'un segment: au compas ou l'aide d'une équerre:

1 Au compas

•  Prendre un écartement de compas plus grand que la moitié du segment
•  Placer la pointe sèche du compas en A et tracer un arc de cercle de part et d'autre du segment
•  Faire de même, pointe sèche en B
• A l'aide d'une règle, tracer une droite reliant M et N, les points d'intersections des arcs de cercle,. cette droite est  la médiatrice de ce segment

2 A l'équerre

• placer le milieu du segment avec la règle graduée 
• tracer avec l'équerre la perpendiculaire au segment passant par le milieu.

Pour savoir comment construire une médiatrice, je vous invite à regarder cette vidéo↓

Priorité Distributivité

 Enchaînement d'Opérations Règles De Priorité

• ​Dans une expression avec des additions et des soustractions et ne comportant pas de parenthèses on effectue l'opération en commençant par la gauche: 

Exemple

A = 7 - 3 + 6

      ↓

A =   4 + 6(on a calculé avant 7 - 2 = 5 et on y a ajouté le 4)

A  =   10

• Dans une expression avec des additions et des soustraction et comportant des parenthèse on commence par calculer l'Expression entre parenthèse

​Exemple: 

B = 8 - (5 - 2)(On calcule avant l'expression entre parenthèse ici

 5 - 2 = 3)

          ↓

B = 8  -  3 (On effectue le reste de l'opération)

B = 5

• Dans une expression sans parenthèses avec des multiplications ou des divisions on commence d'abord par calculer la multiplication ou la division, ensuite on calcule le reste des opérations en partant de la gauche vers la droite.

Exemple:

C = 18 - 2 x 6

           ↓

C = 18 - 12 

C = 6

• Dans une expression avec parenthèse comportant une multiplication ou une division, on commence par calculer l'Expression entre parenthèses, ensuite on effectué l'opération avec la multiplication ou la division , puis le reste en calculant de gauche vers la droite

Exemple: 

D =  44 - 5x( 9 - 2)

D =  44- 5 x 7

D =  44 - 35

D = 9

Entiers et Rationnels

1/ Les nombres entiers

• Les nombres entiers naturels

​Définition

les nombres entiers naturels sont des nombres qui s'écrivent sans virgule, ni barre de fraction ou radical

Exemple: 24;346, 200.....

• Les nombres entiers relatifs

​Définition

Les nombres entiers relatifs sont les nombres positifs et négatifs qui peuvent s'écrire sans virgule , ni  barre de fraction, ni radical...).

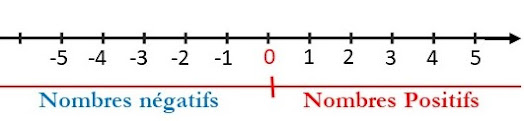
les signes positif (+) et négatif(-) indique la position du nombre sur un axe par rapport à 0

• Les nombres positifs sont situés à droite de 0
• Les nombres négatif sont situés 0 gauche de 0
• Le nombre 0 est le seul nombre qui est à la fois positif et négatif

 

2/Les nombres décimaux

Définition

Un nombre décimal est un nombre composé d'une partie entière comprenant des chiffres situés avant la virgule ; et d'une partie décimale composée de chiffres situés après la virgule.

 Exemple 3,5 ; 56,2 0,507 ....etc

3/ Les nombres Rationnels

Définition

Un nombre « rationnel » est un nombre qui peut s'écrire sous la forme d'un quotient de deux nombres entiers relatifs a/b.

• Multiples Diviseurs :

Définition :

a et b sont deux entiers naturels (non nuls). SI a=b × c avec c un entier ALORS  b est un diviseur de a et a est un multiple de b. Exemple : 15 = 5 × 3 donc 15 est un multiple de 5 ; 15 est divisible par 5 et par 5 et 3 sont appelés diviseurs

• PGCD de deux nombres

Division Euclidienne

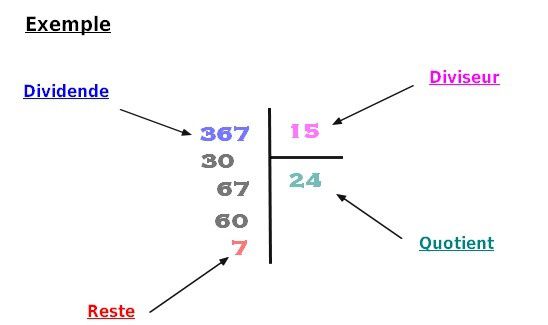
Effectuer une division euclidienne de a par b c'est trouver deux entiers q et r tel que a : b = q + r où r < b  où q est le quotient et r est le reste

a est appelé le dividende et b est le diviseur

 

• Calcul du PGCD 

   Définition

Le PGCD de deux nombres est le plus grand diviseurs commun à ces 2 nombres. On le note PGCD (a ; b)

Pour la méthode de calcul du PGCD, je vous invite à aller voir la ici: PGCD de deux nombres

Cosinus D'un Angle

Définition 

Dans un triangle rectangle, le cosinus d'un angle aigu est égal au quotient du côté adjacent à cet angle (l'angle aigu) sur l'hypoténuse.

 

Le triangle ABC rectangle en B, écrire la formule donnant le cosinus de l'angle  :

- AB  est le côté adjacent à l'angle aigu Â

- AC est l'hypoténuse( le côté le plus grand du triangle)

Donc :

 

Pourquoi utiliser la formule du cosinus?

1. Pour calculer la mesure d'une longueur( côté adjacent d'un angle ou l'hypoténuse).

​Exemple: soit le triangle MNP rectangle en M, l'angle N = 30°,

NP = 6 cm. Calculer la longueur de MN arrondie au dixième près?

Réponse: 

   

 

  

 

2. Pour Calculer la mesure d'un angle

Exemple: Soit un triangle RST rectangle en R, RS = 4 cm, ST = 6 cm

Calculer la mesure de L'angle S au degré?

 

Réponse:

  

 

Pour trouver la mesure de l'angle  il faut utiliser la fonction cos^-1 de la calculatrice. 

Elle s’obtient souvent en tapant sur les touches

 

Dans l'exemple que nous venons de voir pour trouver la mesure de l'angle S, nous avons taper cos^-1(4/6)

 

Remarque: 

La formule du cosinus d’un angle dans un triangle rectangle nous permet de calculer soit la longueur d’un côté(Exemple1), soit un des angles de ce triangle(Exemple2).

 

Bientôt La suite de la leçon, en attendant  entraînez-vous à répondre au Quiz ici

 

 

                            

Les Fonctions affines

 

La fonction affine de coefficients a et b et noté x → ax + b, on la désigne souvent par une lettre par exemple f et on peut la noter aussi sous cette forme: f(x) = ax + b

Exemple: la fonction affine g, de coefficients 3 et -2 s'écrit : g(x) = 3x - 2

Remarque:

• Si b = o, On obtiens une fonction sous la forme de f(x)= ax ce qui correspond à une fonction linéaire. D'où une fonction linéaire est aussi une fonction linéaire avec b = 0

 

• Si a = 0  on obtiens une fonction constante f(x) = b

 

• Si a = b = 0 on obtiens une fonction nulle f(x) = 0

Représentation graphique

Dans un repère, la représentation graphique d'une fonction affine est une droite. l'équation de cette de droite s'écrit sous la forme: y = ax + b.

• x est l'abscisse et y et l'ordonnée
• a s'appelle le coefficient directeur et b s'appelle l'ordonnée à l'origine

 

Exercice d'application: dans un repère, trace la représentation graphique de la fonction affine f x → -x +2

Méthode

• On donne 2 ou 3 valeurs à x supposons 0, 1 et 2
• On calcule leurs images par la fonction f: f(o) = -0 + 2 = 2, f(1) = -1 + 2 = +1, f(2) = - 2 + 2 = 0
• Donc l'image de 0 est 2, l'mage de 1 est - 3 et l'image 2 est -8 

x	0	1	2
f(x)	2	+1	0

 

 

 

Symétrie axiale

Définition

• Deux figures sont symétriques par rapport à une droite si elles se superposent par pliage de la feuille le long de cette droite.

Symétrique d'un point

Définition : On dit que le point A’ est le symétrique du point A par rapport à une droite (d) si la droite (d) est la médiatrice du segment [AA’].

Propriétés:

• Le symétrique d'un segment par rapport à un axe est un segment de même longueur. regardez la Vidéo
• Le symétrique d'un cercle par rapport à un axe est un cercle de même rayon.    Regardez la Vidéo
• La symétrie axiale conserve les longueurs.
• La symétrie axiale conserve les mesures des angles.
• La symétrie axiale conserve l'alignement.

Construction

1. ​Avec l'équerre

                             

• On construit la droite perpendiculaire à (d) et passant par A
• On reporte la distance de A à (d ) de l'autre côté de (d) sur la même perpendiculaire.
• On obtient le point A' qu'on appellera le symétrique de A
• (d) est la médiatrice du segment [AA’].

​

2. Avec le compas