Médiane d'une série statistique
La médiane d'une série statistique est un nombre qui partage
l'effectif en 2 parties égales.
- Déterminer la médiane d'une série
Propriété 1
Si le nombre de valeurs est impair, la médiane est la valeur du milieu
Exemple:
Déterminer la médiane de la série : 11, 4, 9, 7, 6
Il faut d'abord ranger la série dans l'ordre croissant
4 6 7 9 11
Le nombre des valeur est impair alors la médiane est le nombre du milieu de la série
Donc le chiffre 7 est la médiane de cette série car
il partage la série en deux partie égales
Propriété 2
Si le nombre de valeurs est pair, la médiane est
la moyenne des deux valeurs du milieu..
Exemple:
Déterminer la médiane de la série :
1, 2, 57,,
Il faut d'abord ranger la série dans l'ordre croissant
1 2 3 5 7 9
le nombre de valeurs est pair, la médiane est
la moyenne des deux valeurs du milieu. (3 + 5) ÷ 2 = 4
4 est donc la médiane de cette série
Moyenne d'une série
Définition: la moyenne d'une série est égale
au quotient de la somme de toutes les valeurs
de la série sur le nombre total des valeurs
- Déterminer la moyenne d'une série
- On additionne toutes les valeurs de la série
- 5 est le nombre de valeurs
- Comment calculer l'étendue d'une série?
- 15 est la valeur la plus grande
- 3 est la valeur la plus petite
- Le 1er quartile est la petite valeur de la série noté Q1 telle qu’au moins un quart
- le 2e quartile est noté Q2 et représente la médiane de la série
- le 3e quartile est la petite valeur de la série noté Q3 telle qu’au moins un quart (25 %) des valeurs soient inférieures ou égales à Q3



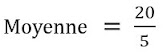


Aucun commentaire:
Enregistrer un commentaire